EMUstack is an open-source simulation package for calculating light propagation through multi-layered stacks of dispersive, lossy, nanostructured, optical media. It implements a generalised scattering matrix method, which extends the physical intuition of thin film optics to complex structures.
Origin
EMUstack is the product of many years research, and is designed primarily as a research tool.
The underpinnings of EMUstack were majoritively developed within CUDOS (the ARC Centre of Excellence for Ultra-high bandwidth Devices for Optical Systems), at its University of Sydney (USyd) and University of Technology Sydney (UTS) nodes.
The scattering matrix method formalism was developed by Lindsay Botten, Ara Asatryan, and Kokou Dossou at UTS. The FEM routine was developed by Kokou Dossou while at the Université du Québec en Outaouais, Université Laval and UTS.
EMUstack was written by Björn Sturmberg during his Ph.D. at USyd, which was supported by the Australian Renewable Energy Agency. THE FEM routine was written by Kokou Dossou, and Felix Lawrence created the smooth f2py interface of Fortran and Python while at UTS.
Approach
At the heart of the scattering matrix approach is the requirement that each layer is uniform in one direction, here labelled z.
In-plane each layer can be homogeneous, periodic in x or y, or double periodic (periodic in x and y). The modes of periodic (structured layers) are calculated using the Finite Element Method in respectively 1 or 2 dimensions, while the modes of homogeneous media are calculated analytically. This approach maximises the speed and accuracy of the calculations. These layers can be stacked in arbitrary order.
Applications
The possible applications of EMUstack are vast.
Below we provide a few examples that demonstrate the unique physical insights and numerical advantages of EMUstack. The calculation of each example is covered on the Tutorial page.
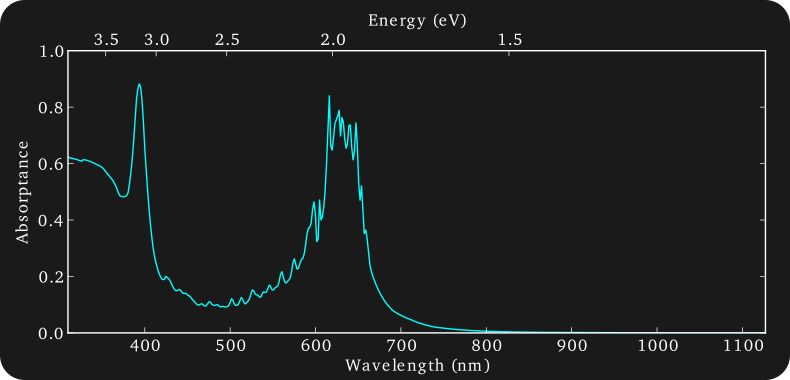
Extraordinary Optical Transmission
Calculation of transmission and reflection through a gold film with square nanoholes. Use dispersive, lossy refractive index of gold from measured tabulated data. Excellent agreement with Rigorous Coupled Wave Analysis (RCWA), with slightly higher transmission. Unlike RCWA we can independently select number of modes in each layer, allowing for a better expansion in the gold nanohole array. EMUstack does also not suffer from Gibbs phenomenon at high refractive index contrast boundaries between gold film and air holes.
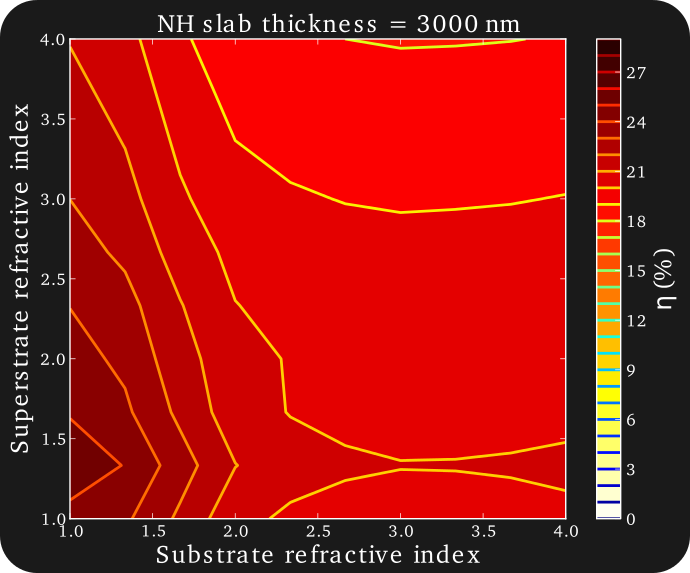
Scan over Superstrate, Substrates, and Height
For each wavelength, the Bloch modes of the nanohole array are computed numerically while the reflection and transmission through the stack are handled semi-analytically. Since the Bloch modes are independent of the superstrate refractive index, substrate refractive index and nanohole array thickness, many different values of these parameters can be efficiently analysed in a single simulation. EMUstack is thus ideally suited to studying the manner in which spectral properties (e.g., conversion efficiency) vary with these parameters.
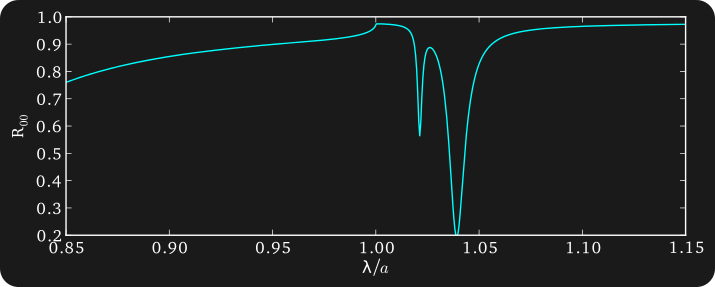
Woodpile Metamaterials
Three dimensional woodpile stacks are typically composed of alternating layers of 2 dimensional grating layers. When these layers consist of square cross-section logs (such that each layer is z-invariant) EMUstack is ideally suited to calculating the transmission through and reflection off the 3D woodpile. Using EMUstack we must only calculate the scattering matrix of a single layer. The scattering matrices of all orientations and in-plane shifts are treated analytically as shifts of the original layer. This results in an extremely efficient calculation.
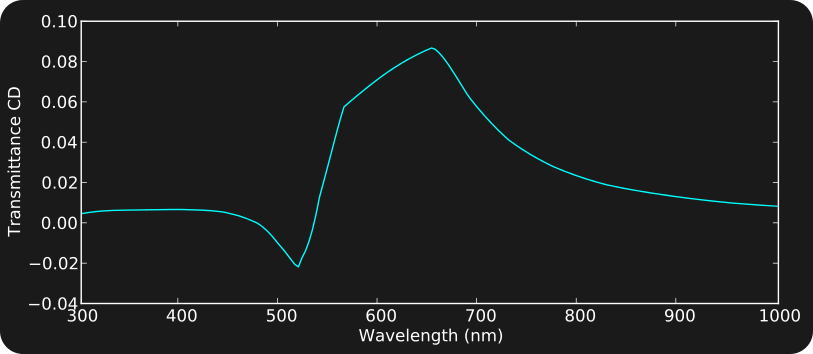
Circular Dichroism in Elliptical Nanohole Arrays
Get both (linear) polarisations in single calculation. Can work out any arbitrary polarisation, including the circular dichroism of the difference between right hand circular polarised and left hand circularly polarised light.